解读AM(振幅调制)合成
解读AM(振幅调制)合成
在《解读模拟合成器『8』--调制器》中,我们讲到了调制的概念,但在那一讲中讲的调制都限制在20Hz这种低频调制的范围内,我们这一讲就说说频率更高的调制。用更高的频率来调制发声源、VCA(压控放大器)、滤波器,这就进入了一个全新的领域:数字合成。
上一讲说到了,当调制源使用更高的频率调制VCA(压控放大器)的振幅时,就称为振幅调制(Amplitude Modulation),简称AM,振幅调制无法使用浅显的语言来形容,我们需要借助数学的力量,向您展示。如果您有初中的数学水平,那么就不要放弃,这些数学真的是很有意思。
请看等式1:
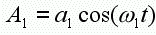 (信号1)
(信号1)
这是一个非常简单的余弦波形,他表示了一个瞬时振幅。(为什么使用余弦而不是正弦做例子呢?因为他们都是完全一样的波形,只是相位有些差别,最主要的是余弦在演算时更为简便)等式1中的t表示时间,a表示振幅,w表示波形的频率。
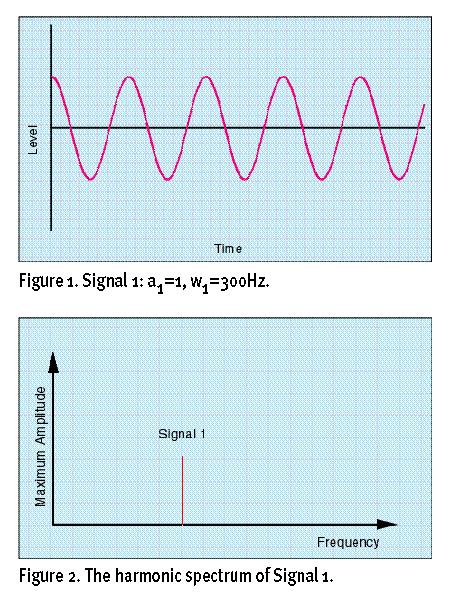
再看等式2:
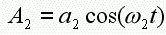 (信号2)
(信号2)
与等式1同为余弦波形,但振幅和频率都改变了。
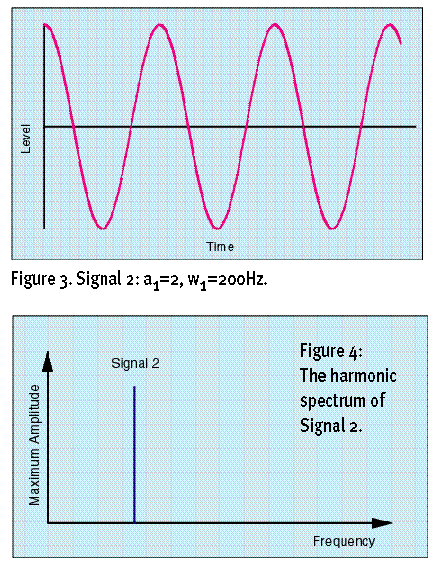
我们假设振幅a1是振幅a2的一半,w1比w2多出一半,也就是说如果w1是300Hz,那么w2就是200Hz。请看图示1(Figure1)和图示3(Figure3),分别是等式1和等式2表示的波形。而图示2(Figure2)和图示4(Figure4)表示了两个波形的谐波频谱。
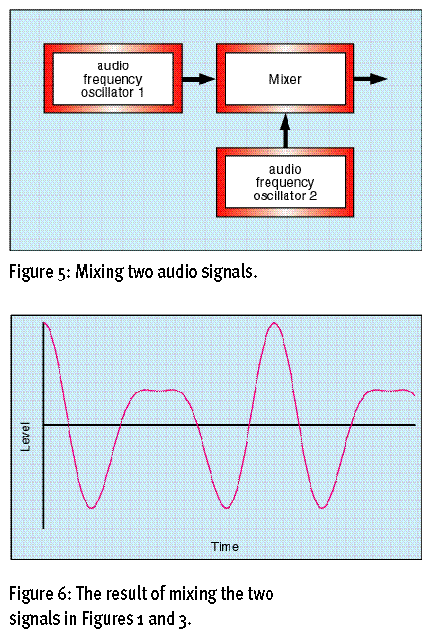
下面让我们看看两个波形混合后的情况,像图示5(Figure5)那样,两个波形同时进入调音台混合,得出了图示6(Figure6)的波形。混合的波形只是将波形的振幅简单的相加。图示7(Figure7)为混合后波形的谐波频谱,其中完全保留了信号1和信号2的频谱。
下面我们将图示5(Figure5)的调音台换成VCA(压控放大器),如图示8(Figure8)那样,保持信号1和信号2的波形不变,只是我们不是将他们简单的混合,而是使用信号2来调制信号1的振幅,这时的信号2就变成了调制器,信号1称为载波器。

使用信号2的波形,来调制信号1波形的振幅,使用等式写出来就是下面的等式3:
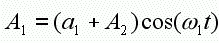
通过等式2我们已经知道A2的波形,所以我们再将等式2带入等式3,就是下面的等式4:
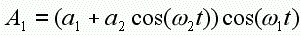
再将a1+a2提出来,就成了等式5:
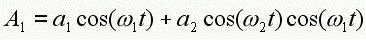
注意等式5加号的后面部分,是两个余弦相乘,这做起来真是非常困难,不过有一个被证明了的数学公理可以派上用场(这可能是在高中时学的,如果不出意外的话你应该全忘了),cosXcosY可以写成cos(X+Y)+cos(X-Y)的形式,对于等式5来说,可以写成以下等式6的形式,这可以看做是振幅调制的结果:
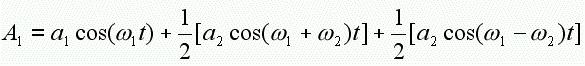
再注意看等式5加号前面部分,其实就是信号1的波形。等式6的两个加号连接了三个式子,每个式子代表了一个波形,那么我们可以说振幅调制的结果就是1个载波器的波形+2个均为一半振幅的调制器的波形,我们称这两个为调制器振幅一半的波形为加信号和减信号。
请看图示9(Figure9),就是通过等式6所示的振幅调制形成的波形,他显然与图示6(Figure6)中使用两个波形简单叠加形成的波形复杂了很多。
图示10(Figure10)显示了振幅调制后的谐波频谱,你发现频谱中只有载波器、加信号和减信号,调制器的信号完全消失了,而加信号和减信号的振幅只有调制器振幅的一半,这显然证实了等式6是完全正确的。

好了,以上就是振幅调制的所有数学理论基础,并不难的对吧?下面我们来看看AM在声音制作中的作用,也许你会问为什么合成器都具有振幅调制的能力呢?假设调制器的频率固定是100Hz,而我们在合成器中按下不同的琴键,也就是使用了不同频率的载波器,会发生什么呢?
第一种情况:载波器和调制器的频率完全一致,都是100Hz。那么振幅调制后的结果是出现了3个频率的声音,0Hz、100Hz、200Hz(通过等式6就可以算出)。你可能天真的以为这个减信号产生的0Hz的频率完全没有用,但是虽然他没有频率,他还是有振幅的(是调制器振幅的一半),他使信号产生了DC(直流)偏移(Direct Current Offset),作用于波形的结果就是有大量波形位于X轴的上面,DC偏移作用于其他模块(比如滤波器、放大器)时会产生更多变化,不过这不在本文的讨论范围之内了。见图示11(Figure11)
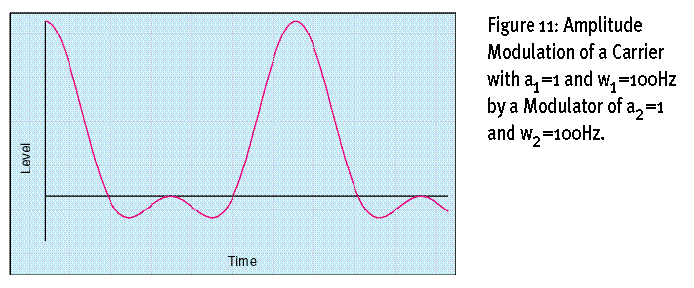
除了0Hz,还有另外的两个信号:载波器的100Hz和加信号的200Hz,加信号整整比载波器高了1个八度,所以声音会比较“甜”。这种情况可以总结为:输出了3个信号,分别是载波器频率的0%、100%、200%。
第二种情况:我们再弹一个高点的音,使载波器频率达到200Hz,而调制器不变还是100Hz。那么加信号和减信号就分别是300Hz和100Hz,减信号几乎比载波器低了一个八度,加信号是减信号的3倍,但是他们发出的声音都盖不过载波器的200Hz。这种情况可以总结为:输出了3个信号,分别是载波器频率的50%、100%、150%。
第三种情况:下面我们找一个不是整百频率的音作为载波器来试试,比如371Hz,那么加信号和减信号就分别为471Hz和271Hz(调制器还是100Hz不变的情况下),这三个音的频率之间都不成整数比,分别是载波器频率的73%、100%、127%。
实际上大多数的音符都不是整百整十的频率,像前两种情况在音乐中基本上是不存在的(没人使用100或200Hz整的音),所以使用振幅调制最多是应用在这些声音上。这时的声音是怎么样的呢?
第四种情况:载波器400Hz,调制器200Hz,那么加信号和减信号就分别是600Hz和200Hz,输出的3个信号分别是载波器频率的50%、100%、150%。
再返回看第二种情况,载波器200Hz,调制器100Hz,那么加信号和减信号就分别是300Hz和100Hz,输出的3个信号分别是载波器频率的50%、100%、150%。
发现什么了吗?两种情况下,载波器与调制器的频率都是2:1的关系,最后输出信号的频率比也是一样的!也就是说不同载波器和调制器频率下,有可能使输出信号波形形状完全一样(只是频率比例不同)。
下面我告诉你振幅调制的真正作用:只使用一个震荡器发出一个波形,经过调制产生更多谐波更复杂的震荡器无法得到的新波形,也就是新的声音。
比如载波器和调制器都是带有一个基波和一个谐波的信号,将他们做振幅调制,会出现一共8个新频率的谐波,这8个新的谐波被称为边带(side bands),见图示12(Figure12)。如果调制器和载波器的波形为2个基波和2个谐波的信号,那么就有18个边带,见图示13(Figure13)。4个基波和4个谐波则会产生多达32个边带。(太多了,不做图了)
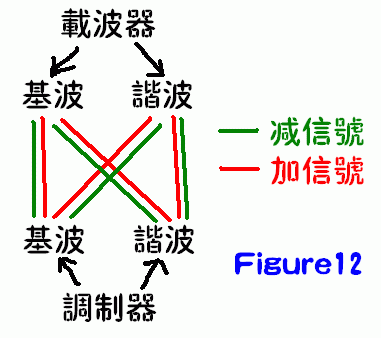
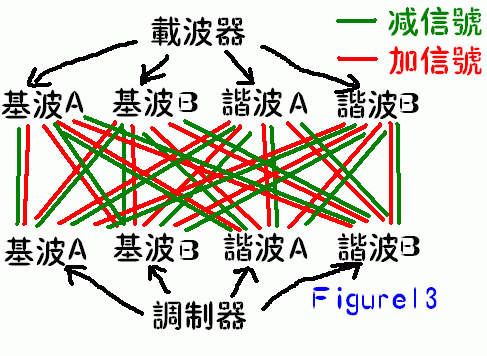
这也就是大家都使用方波和锯齿波作为载波器和调制器波形的原因,锯齿波带有所有一系列常规的谐波,比如一个100Hz的方波就带有100Hz、200Hz、300Hz、400Hz……等等一系列谐波的成分,而一个75Hz的锯齿波则带有75Hz、150Hz、225Hz……等等一系列谐波。那么我们使用75Hz的锯齿波作为调制器去调制100Hz的锯齿波会发生什么?
载波器和调制器的基波首先互相作用,产生25Hz、100Hz、175Hz的信号,而他们的二次谐波再互相作用产生-50Hz、100Hz、250Hz的信号(在这里-50Hz的信号也会发出声音,在你听起来是和50Hz一样的),他们的三次谐波再互相作用产生125Hz、100Hz、325Hz的信号,之后是四次谐波、五次谐波、六次谐波,子子孙孙无穷匮也。
你以为这就完了?还差的多呢!载波器的二次谐波还会与调制器的所有次数的谐波起作用产生信号,之后还有载波器的三次谐波,四次谐波,五次谐波……………………
有一些互相作用而产生的信号非常微弱,可以忽略不计,但是调制后产生的波形还是非常复杂的,但同时也非常悦耳,谐波越丰富,声音就越好听。而且产生的这个新的声音还可以进入合成器的其他模块继续做处理。
以上所说的所有情况都是在完美的VCA下得到的,但是真实的VCA不会将所有的频率都输出出来,最好的VCA设备也达不到,所以调制后输出的声音与实际理论计算出的声音会稍有不同。
环行调制:
环行调制是振幅调制的一个特殊情况,而且他只能作用于载波器和调制器产生0伏信号时。大部分的环行调制都是AC-coupled式的,这意味着在调制之前,DC偏移将被消除掉,但载波器和调制器的自身的频率也无法输出了。还有一种DC-coupled式的环行调制,可以使载波器和调制器的自身的频率也进入输出,有少部分合成器同时提供AC-coupled和DC-coupled,比如ARP 2600。
本文根据《Sound on Sound》杂志的《Synth secrets PART 11:Amplitude Modulation》编译
在《解读模拟合成器『8』--调制器》中,我们讲到了调制的概念,但在那一讲中讲的调制都限制在20Hz这种低频调制的范围内,我们这一讲就说说频率更高的调制。用更高的频率来调制发声源、VCA(压控放大器)、滤波器,这就进入了一个全新的领域:数字合成。
上一讲说到了,当调制源使用更高的频率调制VCA(压控放大器)的振幅时,就称为振幅调制(Amplitude Modulation),简称AM,振幅调制无法使用浅显的语言来形容,我们需要借助数学的力量,向您展示。如果您有初中的数学水平,那么就不要放弃,这些数学真的是很有意思。
请看等式1:
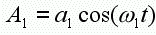 (信号1)
(信号1)这是一个非常简单的余弦波形,他表示了一个瞬时振幅。(为什么使用余弦而不是正弦做例子呢?因为他们都是完全一样的波形,只是相位有些差别,最主要的是余弦在演算时更为简便)等式1中的t表示时间,a表示振幅,w表示波形的频率。
再看等式2:
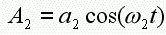 (信号2)
(信号2)与等式1同为余弦波形,但振幅和频率都改变了。
我们假设振幅a1是振幅a2的一半,w1比w2多出一半,也就是说如果w1是300Hz,那么w2就是200Hz。请看图示1(Figure1)和图示3(Figure3),分别是等式1和等式2表示的波形。而图示2(Figure2)和图示4(Figure4)表示了两个波形的谐波频谱。


下面让我们看看两个波形混合后的情况,像图示5(Figure5)那样,两个波形同时进入调音台混合,得出了图示6(Figure6)的波形。混合的波形只是将波形的振幅简单的相加。图示7(Figure7)为混合后波形的谐波频谱,其中完全保留了信号1和信号2的频谱。

下面我们将图示5(Figure5)的调音台换成VCA(压控放大器),如图示8(Figure8)那样,保持信号1和信号2的波形不变,只是我们不是将他们简单的混合,而是使用信号2来调制信号1的振幅,这时的信号2就变成了调制器,信号1称为载波器。

使用信号2的波形,来调制信号1波形的振幅,使用等式写出来就是下面的等式3:
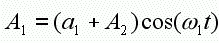
通过等式2我们已经知道A2的波形,所以我们再将等式2带入等式3,就是下面的等式4:
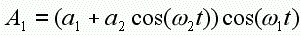
再将a1+a2提出来,就成了等式5:
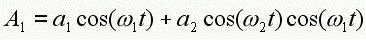
注意等式5加号的后面部分,是两个余弦相乘,这做起来真是非常困难,不过有一个被证明了的数学公理可以派上用场(这可能是在高中时学的,如果不出意外的话你应该全忘了),cosXcosY可以写成cos(X+Y)+cos(X-Y)的形式,对于等式5来说,可以写成以下等式6的形式,这可以看做是振幅调制的结果:
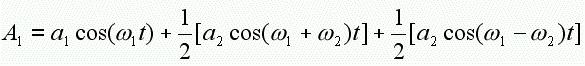
再注意看等式5加号前面部分,其实就是信号1的波形。等式6的两个加号连接了三个式子,每个式子代表了一个波形,那么我们可以说振幅调制的结果就是1个载波器的波形+2个均为一半振幅的调制器的波形,我们称这两个为调制器振幅一半的波形为加信号和减信号。
请看图示9(Figure9),就是通过等式6所示的振幅调制形成的波形,他显然与图示6(Figure6)中使用两个波形简单叠加形成的波形复杂了很多。
图示10(Figure10)显示了振幅调制后的谐波频谱,你发现频谱中只有载波器、加信号和减信号,调制器的信号完全消失了,而加信号和减信号的振幅只有调制器振幅的一半,这显然证实了等式6是完全正确的。

好了,以上就是振幅调制的所有数学理论基础,并不难的对吧?下面我们来看看AM在声音制作中的作用,也许你会问为什么合成器都具有振幅调制的能力呢?假设调制器的频率固定是100Hz,而我们在合成器中按下不同的琴键,也就是使用了不同频率的载波器,会发生什么呢?
第一种情况:载波器和调制器的频率完全一致,都是100Hz。那么振幅调制后的结果是出现了3个频率的声音,0Hz、100Hz、200Hz(通过等式6就可以算出)。你可能天真的以为这个减信号产生的0Hz的频率完全没有用,但是虽然他没有频率,他还是有振幅的(是调制器振幅的一半),他使信号产生了DC(直流)偏移(Direct Current Offset),作用于波形的结果就是有大量波形位于X轴的上面,DC偏移作用于其他模块(比如滤波器、放大器)时会产生更多变化,不过这不在本文的讨论范围之内了。见图示11(Figure11)

除了0Hz,还有另外的两个信号:载波器的100Hz和加信号的200Hz,加信号整整比载波器高了1个八度,所以声音会比较“甜”。这种情况可以总结为:输出了3个信号,分别是载波器频率的0%、100%、200%。
第二种情况:我们再弹一个高点的音,使载波器频率达到200Hz,而调制器不变还是100Hz。那么加信号和减信号就分别是300Hz和100Hz,减信号几乎比载波器低了一个八度,加信号是减信号的3倍,但是他们发出的声音都盖不过载波器的200Hz。这种情况可以总结为:输出了3个信号,分别是载波器频率的50%、100%、150%。
第三种情况:下面我们找一个不是整百频率的音作为载波器来试试,比如371Hz,那么加信号和减信号就分别为471Hz和271Hz(调制器还是100Hz不变的情况下),这三个音的频率之间都不成整数比,分别是载波器频率的73%、100%、127%。
实际上大多数的音符都不是整百整十的频率,像前两种情况在音乐中基本上是不存在的(没人使用100或200Hz整的音),所以使用振幅调制最多是应用在这些声音上。这时的声音是怎么样的呢?
第四种情况:载波器400Hz,调制器200Hz,那么加信号和减信号就分别是600Hz和200Hz,输出的3个信号分别是载波器频率的50%、100%、150%。
再返回看第二种情况,载波器200Hz,调制器100Hz,那么加信号和减信号就分别是300Hz和100Hz,输出的3个信号分别是载波器频率的50%、100%、150%。
发现什么了吗?两种情况下,载波器与调制器的频率都是2:1的关系,最后输出信号的频率比也是一样的!也就是说不同载波器和调制器频率下,有可能使输出信号波形形状完全一样(只是频率比例不同)。
下面我告诉你振幅调制的真正作用:只使用一个震荡器发出一个波形,经过调制产生更多谐波更复杂的震荡器无法得到的新波形,也就是新的声音。
比如载波器和调制器都是带有一个基波和一个谐波的信号,将他们做振幅调制,会出现一共8个新频率的谐波,这8个新的谐波被称为边带(side bands),见图示12(Figure12)。如果调制器和载波器的波形为2个基波和2个谐波的信号,那么就有18个边带,见图示13(Figure13)。4个基波和4个谐波则会产生多达32个边带。(太多了,不做图了)


这也就是大家都使用方波和锯齿波作为载波器和调制器波形的原因,锯齿波带有所有一系列常规的谐波,比如一个100Hz的方波就带有100Hz、200Hz、300Hz、400Hz……等等一系列谐波的成分,而一个75Hz的锯齿波则带有75Hz、150Hz、225Hz……等等一系列谐波。那么我们使用75Hz的锯齿波作为调制器去调制100Hz的锯齿波会发生什么?
载波器和调制器的基波首先互相作用,产生25Hz、100Hz、175Hz的信号,而他们的二次谐波再互相作用产生-50Hz、100Hz、250Hz的信号(在这里-50Hz的信号也会发出声音,在你听起来是和50Hz一样的),他们的三次谐波再互相作用产生125Hz、100Hz、325Hz的信号,之后是四次谐波、五次谐波、六次谐波,子子孙孙无穷匮也。
你以为这就完了?还差的多呢!载波器的二次谐波还会与调制器的所有次数的谐波起作用产生信号,之后还有载波器的三次谐波,四次谐波,五次谐波……………………
有一些互相作用而产生的信号非常微弱,可以忽略不计,但是调制后产生的波形还是非常复杂的,但同时也非常悦耳,谐波越丰富,声音就越好听。而且产生的这个新的声音还可以进入合成器的其他模块继续做处理。
以上所说的所有情况都是在完美的VCA下得到的,但是真实的VCA不会将所有的频率都输出出来,最好的VCA设备也达不到,所以调制后输出的声音与实际理论计算出的声音会稍有不同。
环行调制:
环行调制是振幅调制的一个特殊情况,而且他只能作用于载波器和调制器产生0伏信号时。大部分的环行调制都是AC-coupled式的,这意味着在调制之前,DC偏移将被消除掉,但载波器和调制器的自身的频率也无法输出了。还有一种DC-coupled式的环行调制,可以使载波器和调制器的自身的频率也进入输出,有少部分合成器同时提供AC-coupled和DC-coupled,比如ARP 2600。
本文根据《Sound on Sound》杂志的《Synth secrets PART 11:Amplitude Modulation》编译
文章出处 www.midifan.com
转载文章请注明出自 Midifan.com




